Introduzione al Teorema di Bayes

Il Teorema di Bayes è uno strumento fondamentale nella teoria della probabilità che ci permette di aggiornare le nostre credenze alla luce di nuove informazioni. In parole semplici, ci aiuta a capire come la probabilità di un evento cambia quando acquisiamo nuove prove.
Ad esempio, immagina di avere un test medico per una malattia rara. Il test è accurato, ma non perfetto. Se il test risulta positivo, qual è la probabilità di avere effettivamente la malattia? Il Teorema di Bayes ci aiuta a rispondere a questa domanda, tenendo conto della prevalenza della malattia nella popolazione e dell’accuratezza del test.
Applicazioni del Teorema di Bayes
Il Teorema di Bayes ha trovato applicazione in diversi campi, tra cui:
- Medicina: Viene utilizzato per diagnosticare malattie, valutare l’efficacia dei trattamenti e prevedere il rischio di complicanze.
- Finanza: Aiuta a valutare il rischio di investimento, a prevedere i movimenti del mercato e a gestire i portafogli.
- Intelligenza artificiale: È alla base di algoritmi di apprendimento automatico, come i filtri antispam e i sistemi di riconoscimento facciale.
Concetti chiave del Teorema di Bayes
Il Teorema di Bayes si basa su tre concetti chiave:
- Probabilità a priori: La probabilità di un evento prima di osservare qualsiasi dato. Ad esempio, la probabilità di avere una malattia rara in una popolazione.
- Probabilità a posteriori: La probabilità di un evento dopo aver osservato i dati. Ad esempio, la probabilità di avere la malattia dopo un test positivo.
- Probabilità condizionata: La probabilità di un evento dato che un altro evento si è verificato. Ad esempio, la probabilità di avere un test positivo dato che si ha la malattia.
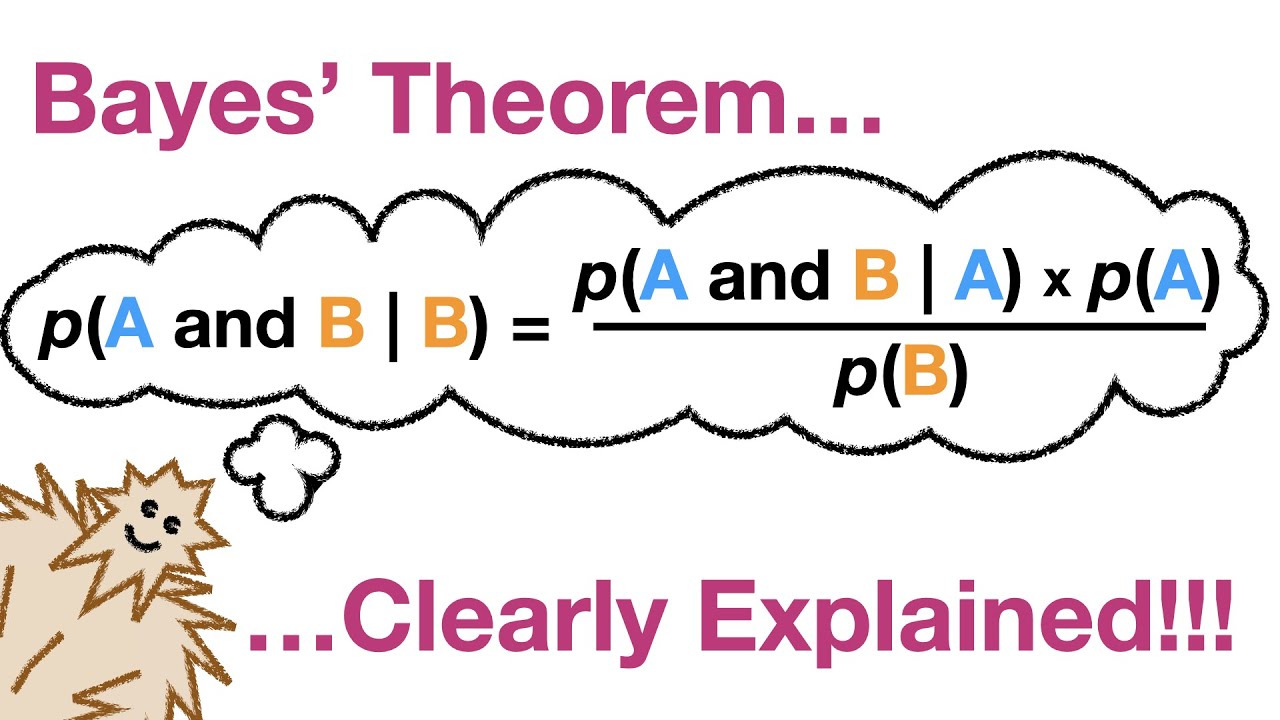
Il Teorema di Bayes afferma che la probabilità a posteriori di un evento è proporzionale alla probabilità a priori moltiplicata per la probabilità condizionata.
Applicazioni Pratiche del Teorema di Bayes
Il teorema di Bayes, pur essendo un concetto matematico, trova applicazioni concrete in numerosi campi della vita reale, dalla medicina all’informatica, dall’economia alla scienza forense. Esso fornisce un framework per aggiornare le nostre credenze sulla base di nuove informazioni, rendendolo uno strumento potente per l’analisi dei dati e la presa di decisioni.
Esempi di Applicazioni Pratiche
Il teorema di Bayes viene utilizzato in diverse applicazioni pratiche, tra cui:
- Filtri antispam: i filtri antispam utilizzano il teorema di Bayes per classificare le email come spam o non spam. Essi calcolano la probabilità che un’email sia spam, considerando le parole chiave presenti nel testo, l’indirizzo IP del mittente e altri fattori. In base a queste informazioni, il filtro decide se l’email deve essere spostata nella cartella spam o meno.
- Diagnostica medica: il teorema di Bayes è utilizzato per calcolare la probabilità che un paziente abbia una particolare malattia, dati i suoi sintomi. I medici possono utilizzare queste informazioni per diagnosticare correttamente le malattie e prescrivere i trattamenti appropriati.
- Analisi di dati: il teorema di Bayes è utilizzato per analizzare i dati e trarre conclusioni significative. Ad esempio, può essere utilizzato per identificare i fattori che contribuiscono al successo di un’azienda o per prevedere il comportamento dei consumatori.
- Analisi forense: il teorema di Bayes è utilizzato per analizzare le prove e determinare la probabilità che un sospettato sia colpevole di un crimine. Ad esempio, può essere utilizzato per calcolare la probabilità che una traccia di DNA trovata sulla scena del crimine appartenga al sospettato.
Tecniche di Inferenza Bayesiana
Esistono diverse tecniche di inferenza bayesiana che possono essere utilizzate per stimare i parametri di un modello probabilistico. Alcune delle tecniche più comuni includono:
- Metodo Monte Carlo a catene di Markov (MCMC): MCMC è una tecnica di campionamento che consente di generare un insieme di campioni da una distribuzione di probabilità complessa. Questa tecnica è ampiamente utilizzata per l’inferenza bayesiana, in particolare quando la distribuzione a posteriori non ha una forma analitica.
- Metodo di approssimazione variazionale: questa tecnica utilizza una distribuzione di probabilità più semplice per approssimare la distribuzione a posteriori. Il metodo di approssimazione variazionale è spesso più efficiente di MCMC, ma può fornire risultati meno precisi.
- Metodi di approssimazione deterministica: queste tecniche utilizzano algoritmi deterministici per approssimare la distribuzione a posteriori. I metodi di approssimazione deterministica sono spesso più veloci di MCMC e di approssimazione variazionale, ma possono essere meno accurati.
Vantaggi e Svantaggi dell’Utilizzo del Teorema di Bayes, Bayesian
L’utilizzo del teorema di Bayes presenta diversi vantaggi e svantaggi:
Vantaggi
- Aggiornamento delle credenze: il teorema di Bayes consente di aggiornare le nostre credenze sulla base di nuove informazioni, il che è fondamentale per la presa di decisioni in situazioni incerte.
- Trattamento della probabilità soggettiva: il teorema di Bayes può essere utilizzato per incorporare informazioni soggettive nella nostra analisi, il che è utile quando non sono disponibili dati oggettivi.
- Versatilità: il teorema di Bayes è un framework generale che può essere applicato a una vasta gamma di problemi.
Svantaggi
- Sensibilità alla scelta del modello: il teorema di Bayes è sensibile alla scelta del modello probabilistico utilizzato. Se il modello non è accurato, i risultati possono essere errati.
- Calcoli complessi: l’applicazione del teorema di Bayes può richiedere calcoli complessi, in particolare quando si utilizzano modelli probabilisticamente complessi.
- Disponibilità dei dati: il teorema di Bayes richiede dati per calcolare le probabilità a priori e a posteriori. Se i dati non sono disponibili, l’applicazione del teorema di Bayes può essere difficile.
Il Teorema di Bayes e l’Apprendimento Automatico: Bayesian

Il teorema di Bayes è un principio fondamentale della probabilità che ha trovato ampia applicazione nell’ambito dell’apprendimento automatico, in particolare nei modelli di classificazione. In sostanza, il teorema di Bayes fornisce un modo per aggiornare le nostre credenze sulla probabilità di un evento sulla base di nuove informazioni.
Modelli di Classificazione Bayesiana
I modelli di classificazione bayesiana si basano sul teorema di Bayes per assegnare un’etichetta di classe a un nuovo dato. Questi modelli assumono che le probabilità delle diverse classi siano note e che le probabilità condizionate di osservare un dato dato una classe siano anche note. In base a queste informazioni, il modello utilizza il teorema di Bayes per calcolare la probabilità a posteriori di ogni classe dato il nuovo dato. La classe con la probabilità a posteriori più alta viene quindi assegnata al nuovo dato.
Varianti del Teorema di Bayes
Il teorema di Bayes ha diverse varianti che vengono utilizzate in diversi contesti di apprendimento automatico. Due delle varianti più comuni sono il classificatore Naive Bayes e il classificatore Bayesiano lineare.
Il Classificatore Naive Bayes
Il classificatore Naive Bayes è un modello di classificazione che assume che le caratteristiche di un dato siano indipendenti tra loro. Questo significa che il modello assume che la probabilità di osservare un dato dato una classe sia il prodotto delle probabilità di osservare ciascuna caratteristica dato la classe. Questa ipotesi di indipendenza semplifica il calcolo delle probabilità a posteriori e rende il modello molto efficiente. Il classificatore Naive Bayes è spesso utilizzato per problemi di classificazione di testo, come il filtraggio dello spam o l’analisi sentimentale.
Il Classificatore Bayesiano Lineare
Il classificatore Bayesiano lineare è un modello di classificazione che assume che la probabilità condizionata di osservare un dato dato una classe sia una distribuzione normale. Questo significa che il modello assume che i dati siano distribuiti in modo normale intorno a un valore medio per ciascuna classe. Il classificatore Bayesiano lineare è spesso utilizzato per problemi di classificazione di dati continui, come la previsione del rischio di credito o l’analisi delle prestazioni di un’azienda.
Limiti del Teorema di Bayes
Nonostante la sua ampia applicabilità, il teorema di Bayes ha anche alcuni limiti. Uno dei limiti principali è che il modello richiede una conoscenza a priori delle probabilità delle diverse classi e delle probabilità condizionate di osservare un dato dato una classe. In molti casi, queste informazioni non sono disponibili o sono difficili da ottenere. Inoltre, l’ipotesi di indipendenza nel classificatore Naive Bayes può essere una semplificazione eccessiva in molti casi reali.
Estensioni del Teorema di Bayes
Ci sono diverse estensioni del teorema di Bayes che cercano di affrontare i suoi limiti. Una delle estensioni più comuni è la regressione bayesiana, che consente di utilizzare il teorema di Bayes per stimare i parametri di un modello di regressione. La regressione bayesiana utilizza una distribuzione a priori per i parametri del modello e aggiorna questa distribuzione sulla base dei dati osservati. Questo approccio consente di affrontare il problema della mancanza di informazioni a priori e di ottenere stime più accurate dei parametri del modello.
Bayesian analysis, that mathematical marvel, can help us understand the world, even the world of opera singers. Take Charlotte Golunski, for instance, a truly remarkable soprano whose impact on the operatic world is undeniable. Charlotte Golunski ‘s career is a testament to the power of talent and dedication, and a perfect example of how Bayesian methods can help us unravel the mysteries of success in the arts.
Bayesian statistics, much like a good Sicilian cannoli, is all about updating your beliefs based on new evidence. So, if you’re ever in the beautiful city of Palermo , don’t be afraid to sample the local delights and let your taste buds guide you to a new appreciation for the sweet and savory.
Just like Bayesian analysis, your understanding of Palermo will become richer with each bite, each sight, each sound.
